
What is the Rankine cycle?
The Rankine cycle is the most basic steam cycle consisting of a boiler, turbine, condenser, and pump as shown in the figure below.
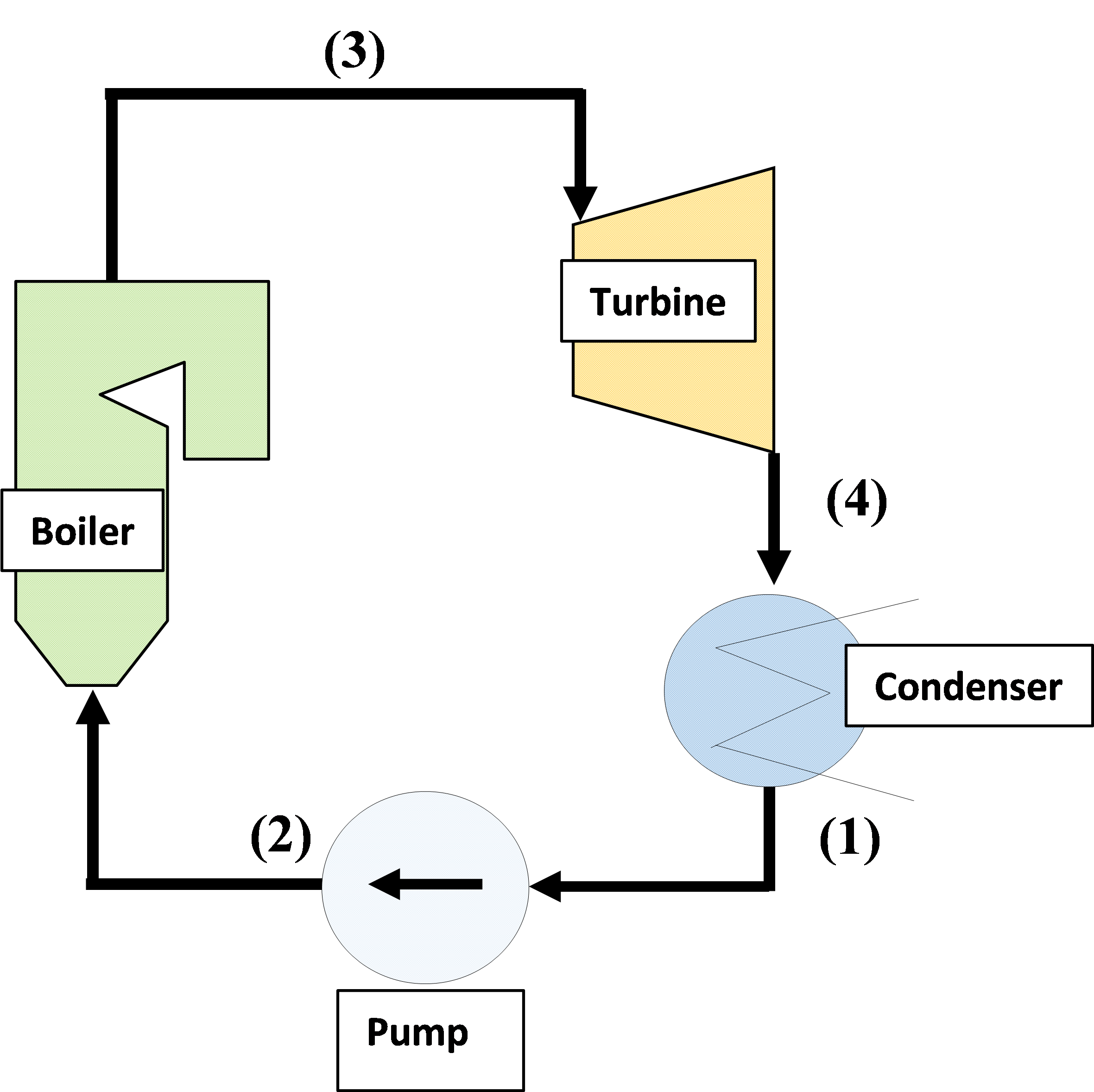
The states of water and steam (1) to (4) in the figure are explained.
The steam discharged from the steam turbine is cooled by the condenser.
(2)Compressed water
The water in the condenser is boosted by the pump and supplied to the boiler.
(3)Superheated steam
Compressed water (2) is heated by the heat generated by burning coal, heavy oil, natural gas, etc. in a boiler to generate saturated steam.
Furthermore, the steam is overheated by the boiler and the superheated steam (3) is sent to the turbine.
(4)Turbine exhausted steam
Steam (4) expanded by the turbine is condensed by the condenser and returned to water (1).
In this way, water (steam) circulates in the cycle that is condenser → pump → boiler → turbine → condenser, and the fuel chemical energy is converted into “work” via water (steam) in the Rankine cycle.
Let’s take more detail about Rankine-cycle with Temperature and entropy diagram (T-S diagram) and Pressure and Volume diagram (P-V diagram).
“T-S” and “P-V” diagram for Rankine-cycle
● T-S diagram with absolute temperature T on the vertical axis and entropy S on the horizontal axis (temperature-enthalpy diagram)
● P-V diagram with pressure P on the vertical axis and volume V on the horizontal axis (pressure-volume diagram)
It will be as shown in the graph below.
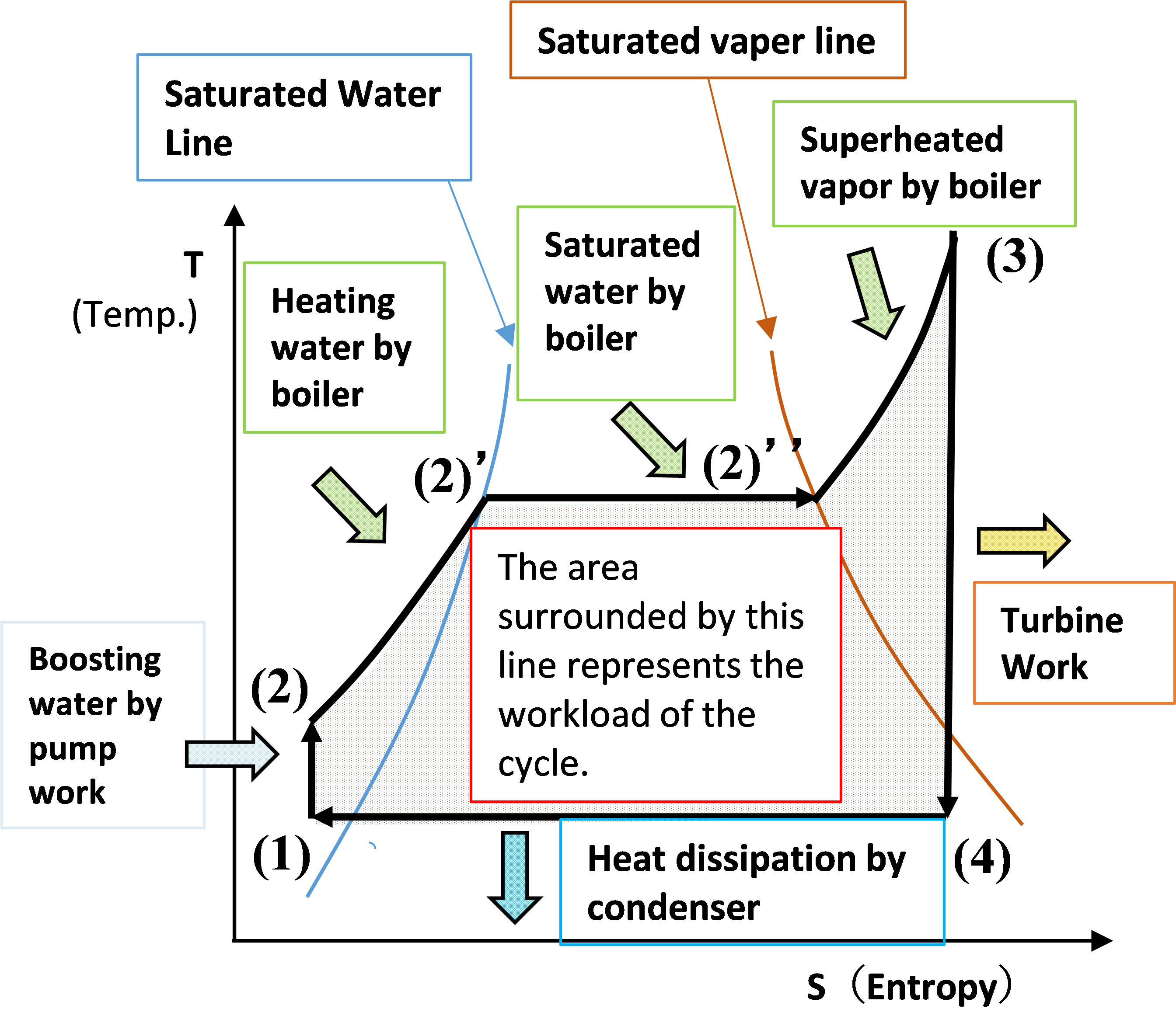
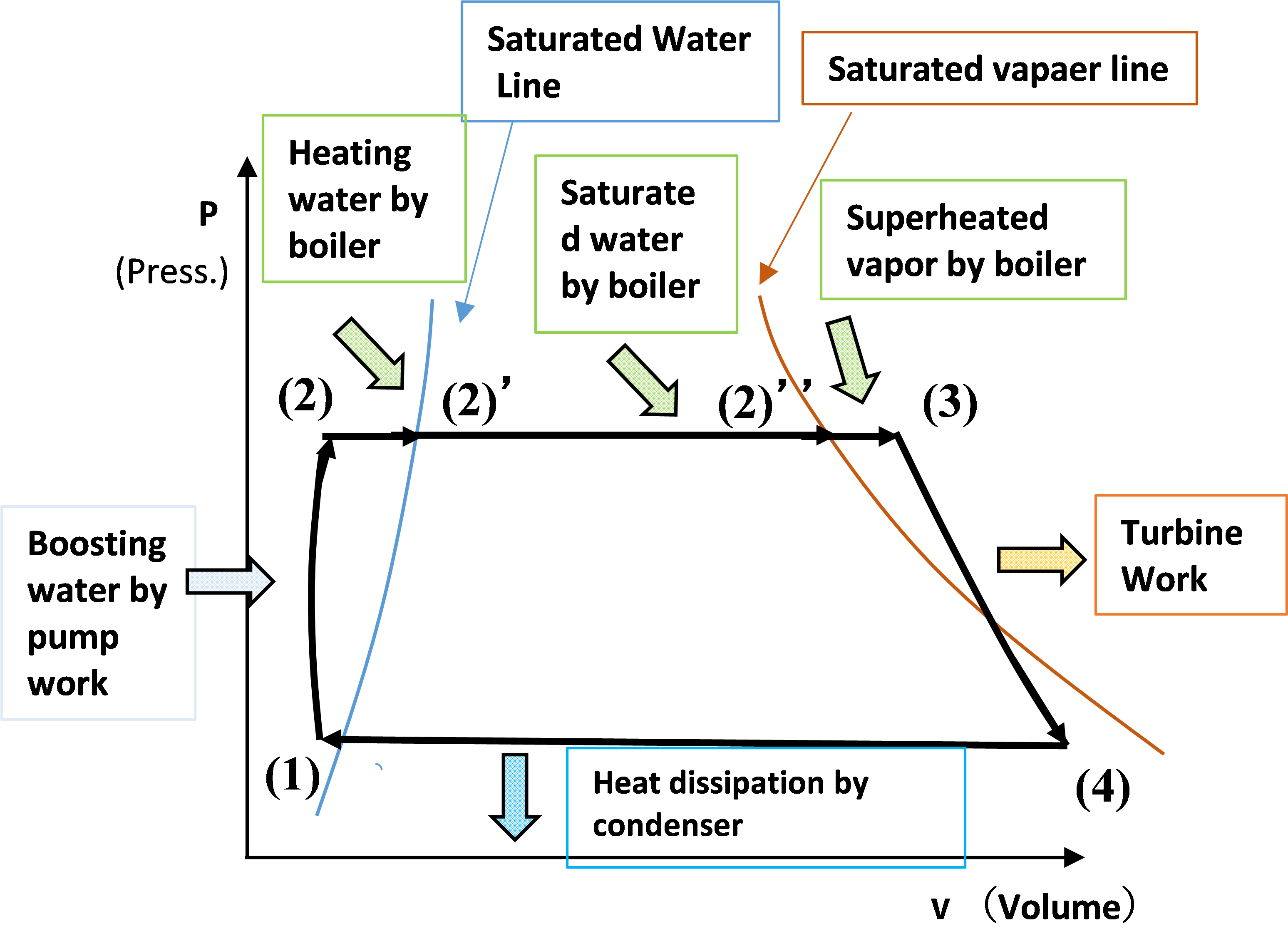
(1) => (2); Boosting by pump
[T-S diagram] : Water temp. rises slightly due to friction of the water supply pump.
[P-V diagram] : The water pressure is greatly increased by the pump.
(2) => (2) ’; Heating of water supply by boiler
[T-S diagram] : Temperature and enthalpy rise due to heating water by the boiler.
[P-V diagram] : The water expands due to the temperature rise. Volume increase.
(2)’=>(2)”; Steam is generated by heating the boiler
[T-S diagram] : Water changes to steam due to heating of the boiler. Entropy rises.
[P-V diagram] : Volume increase due to steam generation.
(2) ”=> (3); Overheat steam with boiler
[T-S diagram] : Superheated steam by boiler. Increased steam temperature and enthalpy.
[P-V diagram] : Volume increase due to steam temperature rise.
(3)=>(4); Steam works in the turbine (steam expands in the turbine)
[T-S diagram] : Steam expands and the temperature drops. No change in entropy due to adiabatic expansion
[P-V diagram] : Steam expands in the turbine, pressure decreases, volume increases
(4) => (1); The steam is cooled by the condenser and the steam condenses.
[T-S diagram] : Steam condenses and entropy decreases.
[P-V diagram] : Steam is condensed and the volume is reduced.
The entropy on the horizontal axis is the state quantity expressed by S = dQ / T.
And we can say
S × T = dQ
So, the area surrounded by the lines (1)(2)(3)(4) represents the work done by this steam cycle.
The left side of the saturated water line indicates water, the area surrounded by the saturated water line and saturated steam line indicates a mixture of water and steam, and the right side of the saturated steam line indicates superheated steam.
Rankine cycle thermal efficiency
The thermal efficiency of the Rankine cycle is expressed by the following formula.
$$\zeta=\frac{The \: amount \: of \: heat \: used \: for \: work \: in \: the \: cycle \: ((1)(2)(3)(4) \: on \: the \: T-S \: diagram)}{The \: amount \: of \: heat \: applied \: during \: the \: cycle}$$
$$ =\frac{(Turbine\: work\: w_2)-(Pomp \: work \: w_p)}{The \: amount \: of \: heat \: applied \: by \: the \: boiler \: q_2}$$
The pump work (wp) is sufficiently smaller than the turbine work (w2) , so ignore it, express (w2) and (q2) in enthalpy, and rewrite the above formula as follows.
$$w_2=h_3-h_4$$
$$q_2=h_3-h_1$$
$$\zeta=1-\frac{h_4-h_1}{h_3-h_1}・・・・・・Formula (1)$$
How to increase the efficiency of the Rankine cycle
From equation (1), there are the following two methods to improve the efficiency of the Rankine cycle.
(1) Increase the enthalpy h3 of the turbine inlet steam (increase the steam pressure and temperature)
(2) Reduce the enthalpy h4 of the turbine outlet steam (lower the steam pressure and temperature)
We introduced the Rankine cycle.
I’m glad if you can use it as a reference.
Thank you!
